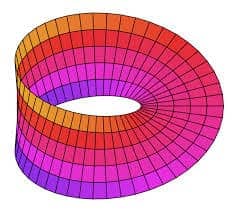
La cinta de moebius

La cinta de moebius (también conocida como banda de moebius, anillo de moebius o möbius), es uno de los objetos geométricos más extraños y curiosos que existen. Sus propiedades, como verás, desafían completamente el sentido común y la lógica.

Se trata de una superficie bidimensional proyectada en un espacio tridimensional, que tiene una sola cara y un solo borde. Por si esto no te ha dejado suficientemente descolocado, también debes saber que es, lo que en matemática se llama, un objeto no orientable, es decir, interior, exterior, arriba, abajo, derecha e izquierda no tienen ningún sentido en este objeto. Si caminas por la superficie de una cinta de moebius sin cambiar de dirección, acabarás en el mismo punto de partida pero cabeza abajo y, si estabas mirando hacia la derecha, te encontrarás mirando hacia la izquierda. Si sigues caminando en la misma dirección, llegarás al punto de partida habiendo recorrido toda la superficie del objeto.

Cual es el origen de este curioso objeto

Los matemáticos alemanes August Ferdinand Möbius (del cual recibe su nombre el anillo en cuestión) y Johann Benedict Listing descubrieron, de forma independiente, la cinta de moebius en el año 1858. Aunque probablemente esta banda se conocía anteriormente, ellos fueron los que desarrollaron las instrucciones para su construcción y describieron sus propiedades.

Construye una cinta de moebius…

Con las extrañas características que hemos descrito de la banda de moebius, podría parecer un objeto más cercano a la abstracción matemática que a la realidad o que para su construcción son necesarias sofisticadas técnicas. En realidad resulta extraordinariamente simple de construir, hasta un niño puede hacerla. Tan solo necesitas una hoja de papel, unas tijeras y pegamento o cinta adhesiva y seguir estos sencillos pasos:

1. Recorta una tira de papel de unos 4 o 5 cm de ancho y unos 30 cm de largo.
2. Forma un aro con la cinta.
3. Gira uno de sus extremos 180º y únelo al otro extremo con cinta adhesiva o pegamento.

Ya has construido una cinta de moebius, sencillo ¿no?

…y experimenta con ella

Ahora que ya has construido tu primera cinta de moebius, puedes realizar algunos experimentos con ella para comprobar sus propiedades.

1. Como ya hemos comentado, el objeto posee tan solo una cara. Para comprobar esta propiedad, coloca la cinta en una superficie plana y coloca la punta de un lápiz o rotulador aproximadamente en el centro de la anchura de la cinta. Presiona ligeramente y ves arrastrando la cinta sin separar el lápiz del papel. Cuando llegues al punto de partida, puedes comprobar cómo ha quedado pintada toda la superficie de la cinta.
2. También sabemos que solo tiene un borde. Haz una marca en el borde, coloca el dedo en la marca y resigue todo el borde. Cuando llegues al punto de partida habrás recorrido la totalidad del borde del objeto sin haber separado el dedo del borde en ningún momento. 
3. Prueba ahora de cortar a lo largo la banda de moebius con las tijeras justo por la mitad del ancho. Obtendrás un solo anillo el doble de largo que el original. Este aro ya no es una cinta de moebius, tiene dos vueltas y vez de media vuelta.
4. Coge otro anillo de moebius y vuelve a cortarlo longitudinalmente, pero esta vez hazlo cerca del borde. Cuando llegues al inicio del corte, tendrás dos anillos entrelazados, uno más largo y otro igual de largo que el original y que sigue siendo una cinta de moebius.
5. Realiza dos anillos de moebius. En el primero realizarás la media vuelta hacia la derecha y en el segundo hacia la izquierda. Ahora une los dos anillos perpendicularmente. Corta los dos anillos por el centro longitudinalmente. El resultado será dos anillos en forma de corazón entrelazados entre sí.

Estos experimentos son tan sencillos que puedes realizarlos con niños. También puedes utilizarlos como trucos de magia para sorprender en reuniones de amigos o familiares. Tan solo tienes que preparar las cintas antes y hacerlas lo suficientemente largas para que no se note la media vuelta.

Las aplicaciones de la banda de moebius

El uso de este enigmático objeto se centra, principalmente, en el ámbito de las matemáticas y, concretamente, en el campo de estudio de la topología. Esto es el estudio de aquellas propiedades de los objetos geométricos que no cambian al someterlos a transformaciones continuas.

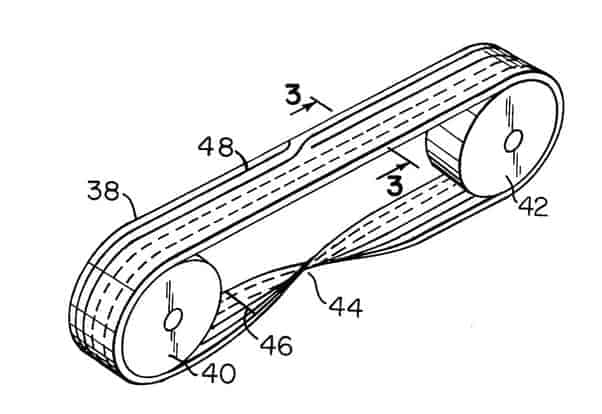
Aun así, existen algunas aplicaciones prácticas en el mundo de la ingeniería. Ya en 1923 se registraba la primera patente para una película que grababa el sonido el doble de tiempo. Este concepto fue utilizado, posteriormente, para la fabricación de cintas magnetofónicas. También se fabrican cintas transportadoras que son una cinta de moebius. De esta manera el desgaste de la superficie es la mitad que en una cinta convencional y, por lo tanto, su vida útil es el doble.

Por otro lado, el símbolo internacional del reciclaje es una banda de moebius que representa el proceso ilimitado del reciclaje de los materiales para darles una nueva vida.

La cinta de Möebius en la ciencia

Investigadores japoneses demostraron en 2002 que los cristales pueden crecer en forma de bandas incluyendo algún giro. Gracias a estos estudios consiguieron sintetizar un conductor inorgánico basado en un cristal con una estructura de anillo de Moebius. Este descubrimiento podría ser útil para el estudio de los efectos topológicos en la mecánica cuántica.

En química se conocen algunas moléculas y proteínas que están relacionadas con la cinta de moebius.

La banda de Möbius en el arte

La banda de Möbius también ha sido y es una fuente de inspiración para artistas de cualquier disciplina. Literatura, cine, pintura, diseño, arquitectura son solo alguna de las artes en que este objeto tan especial ha sido utilizado y reinterpretado.

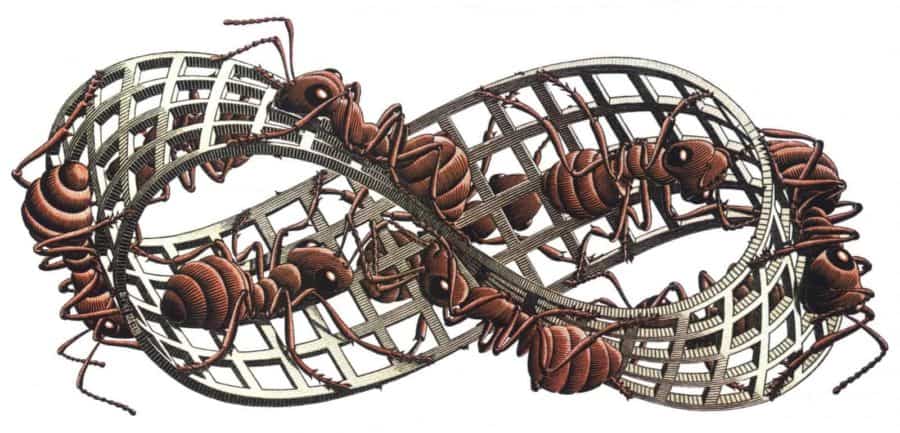
Probablemente la cinta de moebius más conocida del arte sea la de las famosas hormigas del artista neerlandés M. C. Escher. Unas hormigas que parecen estar condenadas a recorrer el anillo hasta el fin de los tiempos. Escher es conocido por sus figuras imposibles, teselados y mundos imaginarios representados en 2 o 3 dimensiones. Creador de entornos paradójicos que confunden la mente humana hasta el punto de no saber lo que es real y lo que no.

Arquitectura, diseño y esculturas con la cinta de moebius

En arquitectura, diseño y escultura también se ha utilizado la banda de moebius en numerosos proyectos. La combinación de formas y curvas sinuosas con el concepto de infinito relacionado con la banda de moebius proporcionan a las obras una gran plasticidad y belleza.

La cinta de moebius en la literatura, el cine y la música

J.S. Bach compuso en 1747 el “Canon del cangrejo”. Se trata de una sencilla pieza que tiene la increíble característica que acaba y empieza en el mismo punto y que puede interpretarse en ambas direcciones. Además, si se superponen, crea un acompañamiento y un conjunto armónico-melódico sin fin. Jos Leys y Xanlox han creado un maravilloso vídeo que fusiona la composición de Bach y el descubrimiento de Moebius.

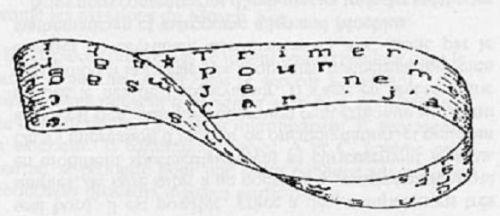
Quién podría creer que incluso en la poesía hace acto de presencia esta formidable cinta. Luc Étienne (1908-1984), un autor francés vinculado al surrealismo, utiliza la cinta de moebius para proponer un nuevo tipo de poesía. Escribe la mitad de un poema en la cara de una banda y la otra mitad en la cara contraria. Al construir, con la banda, una cinta de moebius se genera un nuevo poema con un sentido muy diferente del original.

Imagenes y fotos de la cinta de moebius

Y ya para acabar y como dijo Sheldon Cooper, ¿Por qué la gallina cruzó la cinta de Möbius? Para llegar al mismo lado.